Base Conversion Calculator
Base Conversion Calculator
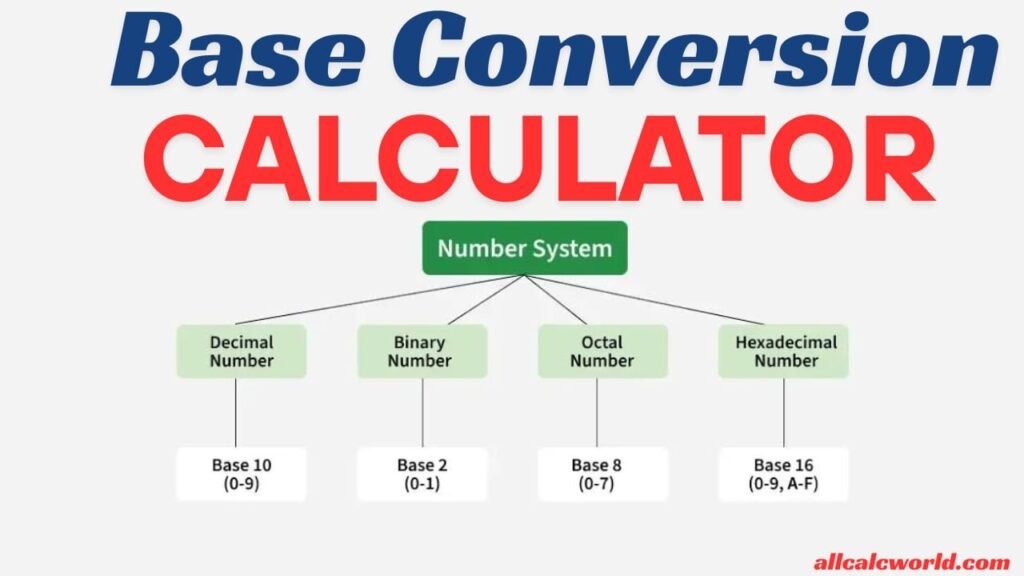
Table of Contents
Number System Base Conversion Calculator: A Simple Guide
In today’s digital world, understanding number systems and how to convert between them is more relevant than ever. Whether you’re a programmer, a math enthusiast, or just curious, number system base conversion is a fascinating topic that bridges computer science, mathematics, and logic. This article dives into what number system base conversion is, why it matters, and how to do it, all while keeping things simple and engaging. Plus, we’ve included a handy FAQ section to answer your burning questions in a humanized, approachable tone.
What Are Number Systems?
At their core, number systems are ways to represent numbers using a specific set of symbols and rules. The “base” of a number system tells you how many unique digits are used. For example:
- Decimal (Base-10): Uses digits 0–9. This is what we use in everyday life (e.g., 42, 123).
- Binary (Base-2): Uses only 0 and 1. Computers love this because it aligns with their on/off logic (e.g., 101010 for 42).
- Octal (Base-8): Uses digits 0–7. It’s less common but useful in certain computing contexts (e.g., 52 for 42).
- Hexadecimal (Base-16): Uses 0–9 and A–F (where A=10, B=11, etc.). It’s popular in programming for compact color codes and memory addresses (e.g., 2A for 42).
Each system is just a different lens for viewing the same value. Base conversion is the process of translating a number from one base to another, like turning 42 (decimal) into 101010 (binary).
Why Is Base Conversion Important?
Base conversion isn’t just academic—it’s practical. Here’s why it matters:
- Programming: Computers operate in binary, but humans find decimal or hexadecimal easier. Converting between bases helps programmers debug code, work with memory, or handle low-level operations.
- Data Representation: Hexadecimal is used in color codes (#FF0000 for red) and memory addresses, while binary underpins all digital systems.
- Problem-Solving: Math and logic puzzles often involve different bases, sharpening your analytical skills.
- Education: Understanding bases builds a foundation for computer science and mathematics.
Whether you’re coding a website or solving a math problem, knowing how to switch between bases is a superpower.
How to Convert Between Number Systems
Let’s break down the process of converting numbers between bases. We’ll focus on converting from any base to decimal (base-10) and from decimal to another base, as these are the building blocks for all conversions.
Converting to Decimal (Base-10)
To convert a number from any base to decimal, use the positional value method. Each digit is multiplied by its base raised to the power of its position (starting from 0 on the right).
Example: Convert 2A (hexadecimal) to decimal.
- 2A means 2 × 16¹ + A × 16⁰.
- A = 10 in decimal, so: 2 × 16 + 10 × 1 = 32 + 10 = 42.
Example: Convert 1101 (binary) to decimal.
- 1101 means 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰.
- That’s 1 × 8 + 1 × 4 + 0 × 2 + 1 × 1 = 8 + 4 + 0 + 1 = 13.
Converting from Decimal to Another Base
To convert a decimal number to another base, divide the number by the target base repeatedly, collecting remainders in reverse order.
Example: Convert 42 (decimal) to binary.
- 42 ÷ 2 = 21, remainder 0.
- 21 ÷ 2 = 10, remainder 1.
- 10 ÷ 2 = 5, remainder 0.
- 5 ÷ 2 = 2, remainder 1.
- 2 ÷ 2 = 1, remainder 0.
- 1 ÷ 2 = 0, remainder 1.
- Read remainders bottom-up: 101010.
Example: Convert 42 (decimal) to hexadecimal.
- 42 ÷ 16 = 2, remainder 10 (10 = A in hex).
- 2 ÷ 16 = 0, remainder 2.
- Read remainders bottom-up: 2A.
Converting Between Non-Decimal Bases
To convert between bases like binary and hexadecimal, first convert to decimal, then to the target base. For example, to convert 1101 (binary) to hexadecimal, first convert to decimal (13), then to hexadecimal (D).
Tips for Easy Base Conversion
- Use Base Conversion Calculatoror Speed: Online tools or custom calculators (like the one you can embed in WordPress) make conversions instant.
- Practice Patterns: Binary numbers often end in 0 or 1, hex uses A–F, and octal stops at 7. Spotting these helps validate your work.
- Double-Check: Convert back to the original base to ensure accuracy.
- Learn Shortcuts: For example, every 4 binary digits map to 1 hexadecimal digit (e.g., 1010 = A).
Why Use a Base Conversion Calculator?
Manually converting bases is great for learning, but it’s time-consuming. A base conversion calculator simplifies the process, especially for large numbers or frequent conversions. Modern calculators, like the one you can code for WordPress, offer:
- Real-Time Results: See conversions as you type.
- Error Checking: Alerts for invalid inputs (e.g., entering “G” in binary).
- User-Friendly Design: Clean interfaces with copyable outputs.
- Versatility: Convert between multiple bases in one go.
FAQs About Number System Base Conversion Calculator
Q: Why do computers use binary instead of decimal?
A: Computers use binary because it’s simple—0s and 1s match the on/off states of electronic circuits. It’s like the language of their hardware, making it super efficient for processing and storage.
Q: Is hexadecimal hard to learn?
A: Not really! It’s just like decimal but with extra “digits” (A–F for 10–15). Once you get the hang of counting in hex, it’s as intuitive as counting to 10. Practice with small numbers first!
Q: Can I convert bases without a calculator?
A: Absolutely, but it takes practice. Use the methods above (to/from decimal) and double-check your work. For quick conversions, a calculator saves time, especially for big numbers.
Q: What’s the easiest way to validate my conversion?
A: Convert the result back to the original base. If you get the same number, you’re golden! For example, if 42 (decimal) becomes 2A (hex), convert 2A back to decimal to confirm it’s 42.
Q: Are there real-world uses for octal?
A: Octal isn’t as common today, but it’s used in some programming contexts, like UNIX file permissions (e.g., 755). It’s less bulky than binary but still computer-friendly.